|
Errata (2. Auflage 2016)
Bitte
Fehler, Verbesserungsvorschläge usw. per Email melden: jens.lienig ifte.de.
ifte.de.
-
S. 59: Unten muss es für $i=5$ $(T=7)$ heißen:
$$0,11209 < e^{-14\/7} = 0,13534$$
Der Nenner des Bruchs im Exponenten muss also 7 statt 2 lauten.
-
S. 68, Abb. 3.4: Der Knoten
W, der das Rad aus den Blöcken C, D, E, F, G
repräsentiert, muss Kindknoten des linken V-Knotens
sein.
-
S. 116: Im Beispiel für die
quadratische Zuordnung muss das Netz zwischen den Zellen 4 und 5
gestrichen werden. Es ist weder Bestandteil der Netzliste noch taucht
es in den angegebenen Matrizen auf.
-
S. 153f.: In Menge 2 müssen die Knoten
W (6) 18,18 und W (8) 12,19
gestrichen werden, sobald mit N (6) 12,19 bzw.
N (8) 12,14 günstigere Wege gefunden werden.
-
S. 164 oben: Die
minimale Spuranzahl eines Kanals entspricht der Knotenanzahl
in der größten Clique im horizontalen Verträglichkeitsgraphen
(HCG) und nicht, wie angegeben, dem längsten Pfad im Graphen.
Eine Clique ist ein Teilgraph des HCG, in dem jeder Knoten mit
jedem anderen Knoten durch eine Kante verbunden ist.
-
S. 205:
In Schritt 5 muss ein Via zur Nachbarebene mit den Kosten (4/5)
in Betracht gezogen werden. Der Rasterpunkt (3/5) links oben in
Ebene 1 muss bereits direkt nach Schritt 5 betrachtet werden
(und nicht erst in Schritt 9), wobei zudem ein Via zur
Nachbarebene mit den Kosten (4/5) eingetragen werden muss. Nach
Schritt 9 muss zunächst der Rasterpunkt (2/6) links in Ebene 2
betrachtet werden. Diese Änderungen haben keine Auswirkungen auf das Ergebnis.
Korrigierte Abbildung (Anklicken zum Vergrößern):
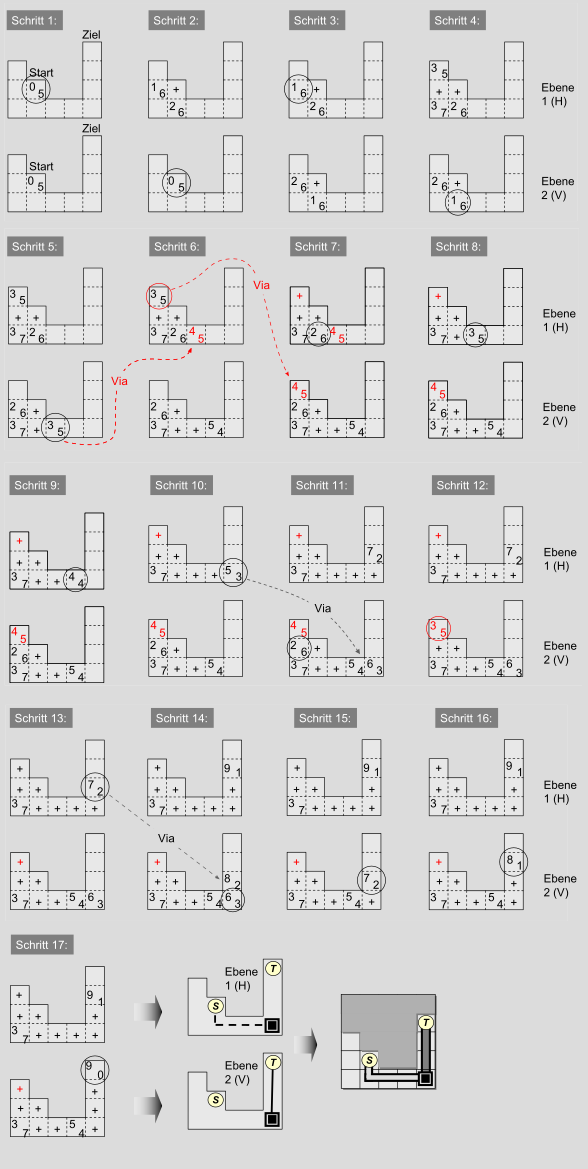
-
S. 215, Abb. 7.22: In den Schritten b, c, e sollte die diagonal
platzierte Zelle zum jeweiligen Startpunkt S mit "2"
(statt "1") markiert sein, die darauf folgende mit "3" (da wir
nur orthogonal routen)
-
S. 254, Aufgabe 3: Im letzten Eintrag in Menge 2 muss
die Richtung W statt N lauten.
|
|
Errata (1. Auflage 2006)
-
S. 59: Die Angaben $a_i$, $b_i$ in der Tabelle sind der Größe
nach sortiert und reflektieren damit nicht die Zuordnung zu den
Partitionen A und B. Partitionsgerechte Zuordnungen sind in den
Schritten wie folgt: 6 (5,1), 8 (6,2), 9 (3,1), 10 (4,3), 12
(6,5), 13 (3,1), 15 (6,1), 16 (2,1).
-
S. 59: Unten muss es für $i=5$ $(T=7)$ heißen:
$$0,11209 < e^{-14\/7} = 0,13534$$
Der Nenner des Bruchs im Exponenten muss also 7 statt 2 lauten.
-
S. 68, Abb. 3.4: Der Knoten
W, der das Rad aus den Blöcken C, D, E, F, G
repräsentiert, muss Kindknoten des linken V-Knotens
sein.
-
-
S. 80, letzter Abschnitt: Bei 100 Blöcken ergeben sich
"über 10.000 Variable" (9.900+200=10.100) und
nicht "über 1000".
-
S. 116: Im Beispiel für die
quadratische Zuordnung muss das Netz zwischen den Zellen 4 und 5
gestrichen werden. Es ist weder Bestandteil der Netzliste noch taucht
es in den angegebenen Matrizen auf.
-
S. 118, oben: Die Gleichungen
sowie die Erklärungen der Matrix $C$ und der Vektoren $K_\text"x"$ und
$K_\text"y"$ sind nicht korrekt. Richtig ist: $$L(P) = 1/2 [X^\text"T"
AX + Y^\text"T" AY] - b_\text"x"^\text"T" X - b_\text"y"^\text"T" X +
k$$ Dabei gilt:
-
$A$ ist eine Matrix mit $A[i][j]=-c_{ij}$ wenn $i≠j$ und $A[i][i]
=$ Summe der Verbindungskosten $c$ der Zelle $i$ (damit entspricht
$A$ der Gesamtkostenmatrix $E$ von S. 116).
-
$X$ ist ein Vektor der Dimension $n$ der $x$-Koordinaten der zu
platzierenden (verschiebbaren) $n$ Zellen.
-
$b_\text"x"$ ist ein Vektor mit $b_\text"x"[i] =$ Summe der $x$-Koordinaten
aller nicht verschiebbaren Zellen und Außenanschlüsse, die mit der
Zelle $i$ verbunden sind.
-
$Y$ ist ein Vektor der Dimension $n$ der $y$-Koordinaten der zu
platzierenden (verschiebbaren) $n$ Zellen.
-
$b_\text"y"$ ist ein Vektor mit $b_\text"y"[i] =$ Summe der $y$-Koordinaten
aller nicht verschiebbaren Zellen und Außenanschlüsse, die mit der
Zelle $i$ verbunden sind.
- $k$ ist eine Konstante.
Das globale Minimum und damit die optimalen $x$- und $y$-Platzierungskoordinaten
der Zellen lassen sich durch die partielle Ableitung von $L(P)$, also
$$\table {∂L(P)}/{∂X}=AX-b_\text"x"=0, \text"und", {∂L(P)}/{∂Y}=AY-b_\text"y"=0$$
bestimmen.
-
S. 153f.: In Menge 2 müssen die Knoten
W (6) 18,18 und W (8) 12,19
gestrichen werden, sobald mit N (6) 12,19 bzw.
N (8) 12,14 günstigere Wege gefunden werden.
-
S. 174, Abb. 6.17a: Netz 1 ist aufgrund der längeren
Vertikalverbindung zusammenzuführen (nicht Netz 3).
-
S. 181, Abb. 6.22: Das vierte Pin rechts unten ist noch
anzuschließen.
-
S. 205:
In Schritt 5 muss ein Via zur Nachbarebene mit den Kosten (4/5)
in Betracht gezogen werden. Zwei Schritte fehlen im angegebenen
Ablauf: Nach Schritt 5 muss zunächst der Rasterpunkt (3/5) links
oben in Ebene 1 betrachtet werden, wobei zudem ein Via zur
Nachbarebene mit den Kosten (4/5) eingetragen werden muss. Nach
Schritt 9 muss zunächst der Rasterpunkt (2/6) links in Ebene 2
betrachtet werden. Diese Änderungen haben keine Auswirkungen auf das Ergebnis.
Korrigierte Abbildung: Siehe Errata der 2. Auflage oben.
-
S. 254, Aufgabe 3: In Menge 2 muss der Knoten
W (5) 7,5 gestrichen werden, sobald mit
N (5) 4,3 ein günstigerer Weg gefunden wird.
Im letzten Eintrag in Menge 2 muss die Richtung W
statt N lauten.
-
S. 257f., Kapitel 7, Aufgabe 2: In Schritt 6 ist ein Via mit
dem Wert 5,3 möglich. In Schritt 10 ist ein Via mit dem Wert
8,1 möglich. Beide haben keine Auswirkung auf das Ergebnis.
|


